FilmStar News 2023 Digest

Technical Issues - Refractive Index with the $NK Function and BASIC TargetsSelect

Additional piecewise examples discussed here. Ambiguity issues discussed here.

There are materials for which no dispersion function (e.g. Lorentz, Cauchy, etc.) is available. In such cases we are forced to deduce n,k at each wavelength. This piecewise fit capability is built into INDEX (for %R/%T measured at with light incident at 0° on the filmed surface) but also available in DESIGN where possibilities include reverse light incidence and multiple angles/polarization states.

Using Gedankenspektrum techniques, we calculate %R & %T vs. λ for known film thickness and add random noise (normal distribution with standard deviation shown below) to the spectra . We then reverse-engineer spectra to deduce n & k vs λ and compare with the known film thickness. Ideally our solution is the already known n,k array we started with.

IMPORTANT: We are concerned here with the accuracy of reverse-engineering. The actual index of thin metal layers is a function of film thickness (Double Dispersion).

Using silver as example, click here to download AgRandom.xlsm (1.4M). Copy a spectrum to the clipboard (in this case corresponding to 2.5 nm Ag). In INDEX click Solve..Paste Spectrum and select Algorithm 1. Note that columns with light green background are noise-free. Pink columns add random noise and blue columns apply smoothing.

' In the DESIGN BASIC code below, TargetsSelect extracts multiple targets at a single wavelength
' Targ$ is repeatedly reopened to select multiple targets at other wavelengths.

Const Targs$ = "C:\Winfilm\Data\TargsTemp.trw"
Const bREV As Boolean = False ' Include reverse reflectance targets?
Const OK$ = " Click OK when done."

Sub Main
    If MsgBox("Click <Copy Spectra> in Excel." & OK$, vbOK, "FORWARD") = vbCancel Then Exit Sub
    DataPaste
    SpecTargets True, "R", 1, 0, "R"
    SpecTargets False, "T", 1, 0, "R"
    If bREV Then
        If MsgBox( "Click <Copy Spectra> in Excel." & OK$, vbOK, "REVERSE") = vbOK Then
            DataPaste
            SpecTargets False, "V", 1, 0, "R"
        End If
    End If
    AxesDraw
    FileSave Targs$ ' Save all targets
    DoSolve
End Sub

Sub DoSolve
    Dim w!, nk$
    For w = 1290 To 310 Step -10
        FileOpen Targs$
        TargetsSelect w
        Optimize
        nk$ = nk$ & CStr(w) & vbTab & IndexCoeff(3, 1) & vbTab & IndexCoeff(3,2) & vbCrLf
    Next w
Clipboard nk$
' Now paste nk$ table into INDEX via File..Paste Table
End Sub

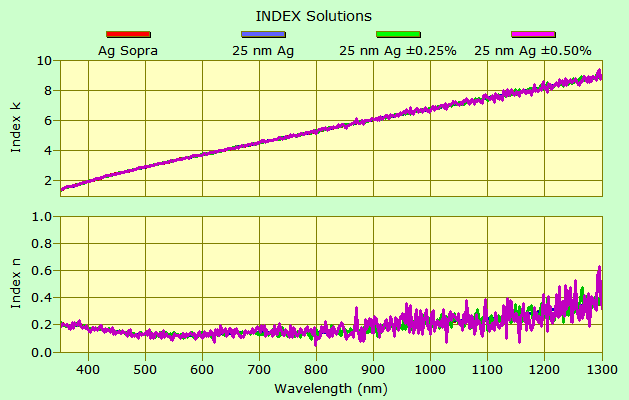
We can also deduce n&k in DESIGN. Below we see that, in the case of 25 nm films, results are essentially identical to INDEX Solutions above. DESIGN adds the ability to include reverse reflectance, angle and polarization. Further work is left to the reader to determine the advantage, if any, to adding reverse reflectance. Graphs shown are based on forward reflectance only.

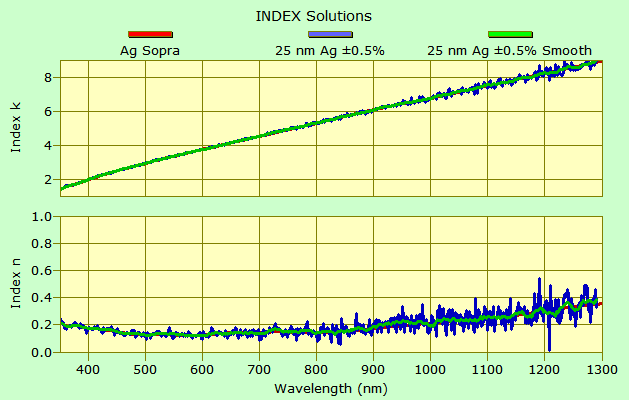
In the following boxcar averaging reduces noise by averaging groups of 11 adjacent spectra.

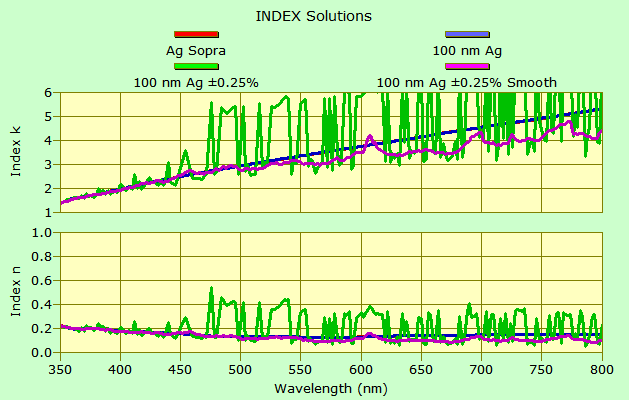
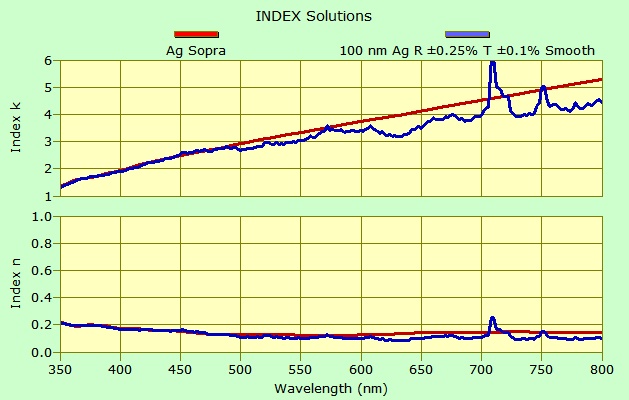
Solutions deteriorate as film thickness becomes large enough to magnify measurement errors. 0.5% variation at T=1% are far more deleterious than at T=80%. As shown below, smoothing helps, but there is no substitute for accurate low-noise measurement techniques.

AgRandom.xlsm includes the possibility of different errors for %R (cell B2) and %T (cell B3) as shown below. Note the peaks at about 710 and 750 nm.

It appears that the peaks correspond to %T noise at 710 and 750. Unfortunately, when %T gets near zero, the effects of random errors are magnified.

The replacement of absolute error by relative error is left to the reader. Current FilmStar users puzzled by any of the above should contact FTG Software for an online presentation.

Further discussion can be found in Willey's Practical Design of Optical Thin Films, Chapter 6 (Finding Indices).